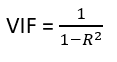What is Multicollinearity? Here’s Everything You Need to Know 

Introduction

Multicollinearity might be a handful to pronounce but it’s a topic you should be aware of in the machine learning field. I am familiar with it because of my statistics background but I’ve seen a lot of professionals unaware that multicollinearity exists.

This is especially prevalent in those machine learning folks who come from a non-mathematical background. And while yes, multicollinearity might not be the most crucial topic to grasp in your journey, it’s still important enough to learn. Especially if you’re sitting for data scientist interviews!

So in this article, we will understand what multicollinearity is, why it’s a problem, what causes multicollinearity, and then understand how to detect and fix multicollinearity.

Table of Contents

• What is Multicollinearity?
• The Problem with having Multicollinearity
• What causes Multicollinearity?
• Detecting Multicollinearity with VIF
• Fixing Multicollinearity

 

What is Multicollinearity?

Multicollinearity occurs when two or more independent variables are highly correlated with one another in a regression model.

This means that an independent variable can be predicted from another independent variable in a regression model. For example, height and weight, household income and water consumption, mileage and price of a car, study time and leisure time, etc.

Let me take a simple example from our everyday life to explain this. Colin loves watching television while munching on chips. The more television he watches, the more chips he eats and the happier he gets!

Now, if we could quantify happiness and measure Colin’s happiness while he’s busy doing his favorite activity, which do you think would have a greater impact on his happiness? Having chips or watching television? That’s difficult to determine because the moment we try to measure Colin’s happiness from eating chips, he starts watching television. And the moment we try to measure his happiness from watching television, he starts eating chips.

Eating chips and watching television are highly correlated in the case of Colin and we cannot individually determine the impact of the individual activities on his happiness. This is the multicollinearity problem!

So why should you worry about multicollinearity in the machine learning context? Let’s answer that question next.

 

The Problem with having Multicollinearity

Multicollinearity can be a problem in a regression model because we would not be able to distinguish between the individual effects of the independent variables on the dependent variable. For example, let’s assume that in the following linear equation:

Y = W0+W1*X1+W2*X2

Coefficient W1 is the increase in Y for a unit increase in X1 while keeping X2 constant. But since X1 and X2 are highly correlated, changes in X1 would also cause changes in X2 and we would not be able to see their individual effect on Y.

“ This makes the effects of X1 on Y difficult to distinguish from the effects of X2 on Y. ”

Multicollinearity may not affect the accuracy of the model as much. But we might lose reliability in determining the effects of individual features in your model – and that can be a problem when it comes to interpretability.

 

What causes Multicollinearity?

Multicollinearity could occur due to the following problems:

• Multicollinearity could exist because of the problems in the dataset at the time of creation. These problems could be because of poorly designed experiments, highly observational data, or the inability to manipulate the data:
  • For example, determining the electricity consumption of a household from the household income and the number of electrical appliances. Here, we know that the number of electrical appliances in a household will increase with household income. However, this cannot be removed from the dataset

• Multicollinearity could also occur when new variables are created which are dependent on other variables:
  • For example, creating a variable for BMI from the height and weight variables would include redundant information in the model

• Including identical variables in the dataset:
  • For example, including variables for temperature in Fahrenheit and temperature in Celsius

• Inaccurate use of dummy variables can also cause a multicollinearity problem. This is called the Dummy variable trap:
  • For example, in a dataset containing the status of marriage variable with two unique values: ‘married’, ’single’. Creating dummy variables for both of them would include redundant information. We can make do with only one variable containing 0/1 for ‘married’/’single’ status.

• Insufficient data in some cases can also cause multicollinearity problems

 

Detecting Multicollinearity using VIF

Let’s try detecting multicollinearity in a dataset to give you a flavor of what can go wrong.

I have created a dataset determining the salary of a person in a company based on the following features:

• Gender (0 – female, 1- male)
• Age
• Years of service (Years spent working in the company)
• Education level (0 – no formal education, 1 – under-graduation, 2 – post-graduation)

	df=pd.read_csv(r'C:/Users/Dell/Desktop/salary.csv')
	df.head()

Multicollinearity can be detected via various methods. In this article, we will focus on the most common one – VIF (Variable Inflation Factors).

” VIF determines the strength of the correlation between the independent variables. It is predicted by taking a variable and regressing it against every other variable. “

or

VIF score of an independent variable represents how well the variable is explained by other independent variables.

R^2 value is determined to find out how well an independent variable is described by the other independent variables. A high value of R^2 means that the variable is highly correlated with the other variables. This is captured by the VIF which is denoted below:

So, the closer the R^2 value to 1, the higher the value of VIF and the higher the multicollinearity with the particular independent variable.

	# Import library for VIF
	from statsmodels.stats.outliers_influence import variance_inflation_factor
	def calc_vif(X):
	# Calculating VIF
	vif = pd.DataFrame()
	vif["variables"] = X.columns
	vif["VIF"] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]
	return(vif)

• VIF starts at 1 and has no upper limit
• VIF = 1, no correlation between the independent variable and the other variables
• VIF exceeding 5 or 10 indicates high multicollinearity between this independent variable and the others

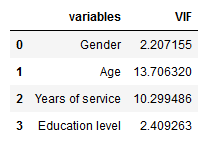
	X = df.iloc[:,:-1]
	calc_vif(X)

We can see here that the ‘Age’ and ‘Years of service’ have a high VIF value, meaning they can be predicted by other independent variables in the dataset.

Although correlation matrix and scatter plots can also be used to find multicollinearity, their findings only show the bivariate relationship between the independent variables. VIF is preferred as it can show the correlation of a variable with a group of other variables.

 

Fixing Multicollinearity

Dropping one of the correlated features will help in bringing down the multicollinearity between correlated features:

	X = df.drop(['Age','Salary'],axis=1)
	calc_vif(X)

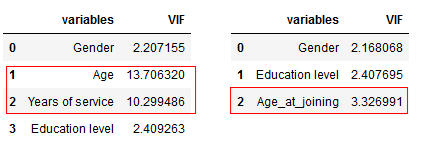
The image on the left contains the original VIF value for variables and the one on the right is after dropping the ‘Age’ variable.

We were able to drop the variable ‘Age’ from the dataset because its information was being captured by the ‘Years of service’ variable. This has reduced the redundancy in our dataset.

Dropping variables should be an iterative process starting with the variable having the largest VIF value because its trend is highly captured by other variables. If you do this, you will notice that VIF values for other variables would have reduced too, although to a varying extent.

In our example, after dropping the ‘Age’ variable, VIF values for all the variables have decreased to a varying extent.

Next, combine the correlated variables into one and drop the others. This will reduce the multicollinearity:

	df2 = df.copy()
	df2['Age_at_joining'] = df.apply(lambda x: x['Age'] - x['Years of service'],axis=1)
	X = df2.drop(['Age','Years of service','Salary'],axis=1)
	calc_vif(X)

The image on the left contains the original VIF value for variables and the one on the right is after combining the ‘Age’ and ‘Years of service’ variable. Combining ‘Age’ and ‘Years of experience’  into a single variable ‘Age_at_joining’ allows us to capture the information in both the variables.

However, multicollinearity may not be a problem every time. The need to fix multicollinearity depends primarily on the below reasons:

1. When you care more about how much each individual feature rather than a group of features affects the target variable, then removing multicollinearity may be a good option
2. If multicollinearity is not present in the features you are interested in, then multicollinearity may not be a problem.